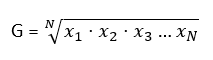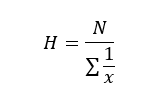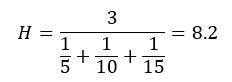Zašto prosjek ocjena ne smijete računati aritmetičkom sredinom?

Računanje aritmetičke sredine je svuda oko nas. Kolika je cijena prosječnog deterdženta? Koliko je visok prosječni učenik 2. razreda? Kolika je prosječna težina muškarca? Gotovo instinktivno svi posežemo za aritmetičkom sredinom da bi došli do odgovora. Zbrajamo rezultate i dijelimo ih s brojem rezultata koje smo prikupili.
Ako ste imali priliku slušati osnove statistike vjerojatno se čuli za mjere središnje vrijednosti i sada znate kako je aritmetička sredina jedna od njih. Uostalom, ne zvuči li nam čudno kada pročitamo da npr. prosječna riječka obitelj ima samo 2.51 člana?
Primjena iskrivljene statistike toliko je postala učestala da više ni statističari ne obraćaju previše pozornosti na krive natpise u novinama. Manipulacija statistikom i cherry picking u službi su svake političke stranke i prikazivanja rezultata minulog rada. Na našu nesreću s politikom ne prestaje kraj krive primjene statistike.
Jedan od prvih susreta sa računanjem prosjeka, gotovo svima nama, je računanje naše prosječne ocjene u osnovnoj školi. Krajem polugodišta nervozno bi zbrajali sve ocjene i dijelili ih s brojem istih u nadi da će prva znamenka iza zareza biti veća od 5, pa ćemo pobjedonosno moći ustvrditi kako smo neoborivo dokazali da zaslužujemo veću ocjenu. Na žalost, niti naši profesori u većini slučajeva nisu imali bolje metode računanja prosjeka.
Nekoliko je problema s takvim zaključivanjem ocjena koje nam odmah padaju na pamet. Vrijedi li jednako ocjena iz zalaganja i ocjena s najtežeg testa? Ne treba li vrednovati učenikova poboljšanja kroz godinu? Jesu li sva područja, tj. svi ispiti, jednako vrijedni? Kao što vidimo, ovo su samo neki od hrpe faktora koje bi najpošteniji sustav ocjenjivanja trebao imati u sebi.
Odrediti takav sustav daleko je izvan područja kojim ćemo se baviti u ovom članku. Ovdje ćemo uzeti statistički pogled na računanje aritmetičke sredine (i ostalih središnjih vrijednosti) i reći zašto tu središnju vrijednost nije dobro koristiti kod računanja prosjeka ocjena.
Aritmetička sredina
Aritmetička sredina ne samo da je najčešća i najpoznatija središnja vrijednost, ona je za mnoge i jedina mjera središnje vrijednosti.
Formulu pri kojoj računamo aritmetičku sredinu već smo spomenuli, no da bi mogli primjenjivati aritmetičku sredinu moramo zadovoljiti još nekoliko uvjeta.
- Rezultati moraju biti prave mjerne vrijednosti, dobivene barem na intervalnoj ljestvici
U statistici poznajemo četiri vrste ljestvica: nominalne, ordinalne, intervalne i omjerne. Intervalna ljestvica pridružuje brojeve mjernim svojstvima elemenata statističkih skupova pri čemu jednake razlike brojeva na mjernoj ljestvici predstavljaju jednake razlike mjernog svojstva. Omjeri u intervalnoj ljestvici nemaju smisla. Dobri primjer intervalne ljestvice je npr. temperatura zbog relativne nule.
- Svi rezultati moraju biti rezultati istovrsnog mjerenja, dakle dobiveni u jednakim uvjetima mjerenja
- Određivanje aritmetičke sredine zahtjeva dovoljan broj rezultata, a to je najmanje 30
- Distribucija rezultata mora biti normalna, što ujedno znači i simetrična
Normalna (Gaussova) distribucija ili razdioba najčešće je korištena teoretska distribucija u statističkim analizama. Da bi neka distribucija rezultata bila normalna ona treba biti simetrična i imati poznati zvonoliki oblik.
Ostale središnje vrijednosti
Medijan
Medijan ćemo upotrijebiti ako u našem skupu rezultata imamo ekstremno veliku ili ekstremno malu vrijednost, odnosno ako je distribucija rezultata asimetrična.
Dobar primjer za računanje medijana su plaće nogometaša u SAD-u. Američki klubovi imaju tendenciju uzimanja najboljih europskih igrača na zalasku karijere, a za uzvrat tim nogometašima daju izdašne ugovore. Njihovi mlađi nepoznati kolege nisu te sreće. Uzmimo za primjer ovogodišnje plaće nogometaša New York City FC-a.
Aritmetička sredina nam govori kako je prosječna plaća igrača New York City FC-a 767.615,55 dolara, no ako bacimo pogled na tablicu vidimo kako samo trojica nogometaša imaju viša primanja od „prosječne“ plaće. Evidentno, aritmetičku sredinu ne smijemo koristiti.
| Igrač | Plaća |
| Frank Lampard | $6,000,000 |
| Andrea Pirlo | $5,600,000 |
| David Villa | $5,610,000 |
| Mix Diskerud | $761,250 |
| Maxime Chanot | $350,004 |
| Frederic Brillant | $260,000 |
| Jefferson Mena | $220,000 |
| Jason Hernandez | $200,000 |
| Andoni Iraola | $200,004 |
| Ronald Matarrita | $150,000 |
| Jack Harrison | $125,000 |
| Josh Saunders | $150,000 |
| Diego Martinez | $135,000 |
| Federico Bravo | $110,000 |
| Khiry Shelton | $77,000 |
| Tony Taylor | $82,500 |
| Mehdi Ballouchy | $71,663 |
| Thomas McNamara | $73,500 |
| Ryan Meara | $75,246 |
| Kwadwo Poku | $67,500 |
| RJ Allen | $63,000 |
| Andre Rawls | $62,508 |
| Eirik Johansen | $62,500 |
| Ethan White | $62,500 |
| Connor Brandt | $53,472 |
| Shannon Gomez | $51,500 |
| Mikey Lopez | $51,500 |
Kako bi izračunali medijan trebamo poredati igrače prema visini primanja i uzeti igrača koji se nalazi u sredini. U našem slučaju to je Frederico Bravo, a prosječna plaća igrača New York City FC-a iznosi $110,000.
Dominantna vrijednost ili MOD (D)
Dominantna vrijednost ili MOD je vrijednost koja se najčešće pojavljuje u skupini prikupljenih rezultata.
Na početku članka spomenuli smo kako prosječna riječka obitelj ima 2.51 člana. Istu grešku nalazimo i kod prosjeka broja djece u kućanstvima. Kako ne bi morali komadati članove obitelji, bolja mjera središnje tendencije u tim slučajevima je dominantna vrijednost.
Geometrijska sredina
Definiramo ju kao n-ti korijen iz umnoška svih članova skupa.
Najviše ju koristimo kada računamo prosječnu brzinu nekih promjena, a ne možemo ju računati ako je bilo koji broj negativan ili nula.
Na primjer, ako je neko mjesto g. 1960. imalo 2000 stanovnika, g. 1961. 9000, a g. 1962. 18 000 stanovnika, onda je populacija g. 1961. bila 4.5 veća od populacije u g. 1960., a populacija godine 1962. dva puta veća od g. 1961. Postavimo li pitanje koliko je puta prosječno populacija svake godine porasla, izračunat ćemo to pomoću geometrijske sredine i dobiti da je porasla 3 puta, što odgovara stvarnom stanju.
Harmonična sredina
Upotrebljavamo ju kada želimo dobiti prosjeke nekih odnosa (npr. prosječne kilometre na sat, prosječan broj slova napisanih u minuti).
Računamo ju prema formuli:
Zamislite da smo pitali 3 osobe da nam kažu koliko dugo im traje staklenka od 1 kg marmelade. Odgovore koje smo dobili su sljedeći:
- osoba – 5 dana
- osoba – 10 dana
- osoba – 15 dana
Pitanje: Koliko prosječno u ta tri domaćinstva traje 1 kg marmelade? Ne, nije točno da taje 10 dana iako to djeluje logično.
Prvo pogledajmo koliko staklenki te osobe potroše u 30 dana:
- osoba 6 staklenki
- osoba 3 staklenke
- osoba 2 staklenke
Dakle, 11 kg marmelade u 30 dana, što znači da 1 kg traje u prosjeku 30/11 = 2.727 za sve tri osobe zajedno. Za jednu osobu, dakle, 1 kg traje dulje, tj. u prosjeku 2.727*3 = 8.2 dana
Provjerimo li logiku računom harmonične sredine dobijemo:
Ni harmonična sredina se ne može izračunati ako je bilo koji broj negativan ili nula.